Why Is Statistical Significance Important?
Discover why statistical significance matters in data analysis, research, and business decisions. Learn about p-values, hypothesis testing, and how to interpret...
Learn how statistical significance determines whether results are real or due to chance. Understand p-values, hypothesis testing, and practical applications for your business in 2025.
Statistical significance is used to determine whether a result is by chance or caused by some factor of interest. If statistically significant, it is unlikely to have occurred by chance.
Statistical significance is a fundamental concept in data analysis that helps you distinguish between genuine effects and random fluctuations in your data. When you conduct experiments, surveys, or analyze business metrics, you need a reliable method to determine whether the patterns you observe are real or simply the result of chance. Statistical significance provides this critical framework by using mathematical principles to assess the probability that your observed results would occur if there were truly no effect or difference between the groups you’re comparing.
The concept emerged from the work of statistician Ronald Fisher in the early 20th century and has become the cornerstone of hypothesis testing across virtually every field that relies on data analysis. From pharmaceutical research validating new drug treatments to e-commerce companies optimizing conversion rates, statistical significance serves as the gatekeeper between actionable insights and misleading conclusions. Understanding how statistical significance works empowers you to make informed decisions backed by solid evidence rather than intuition or coincidence.
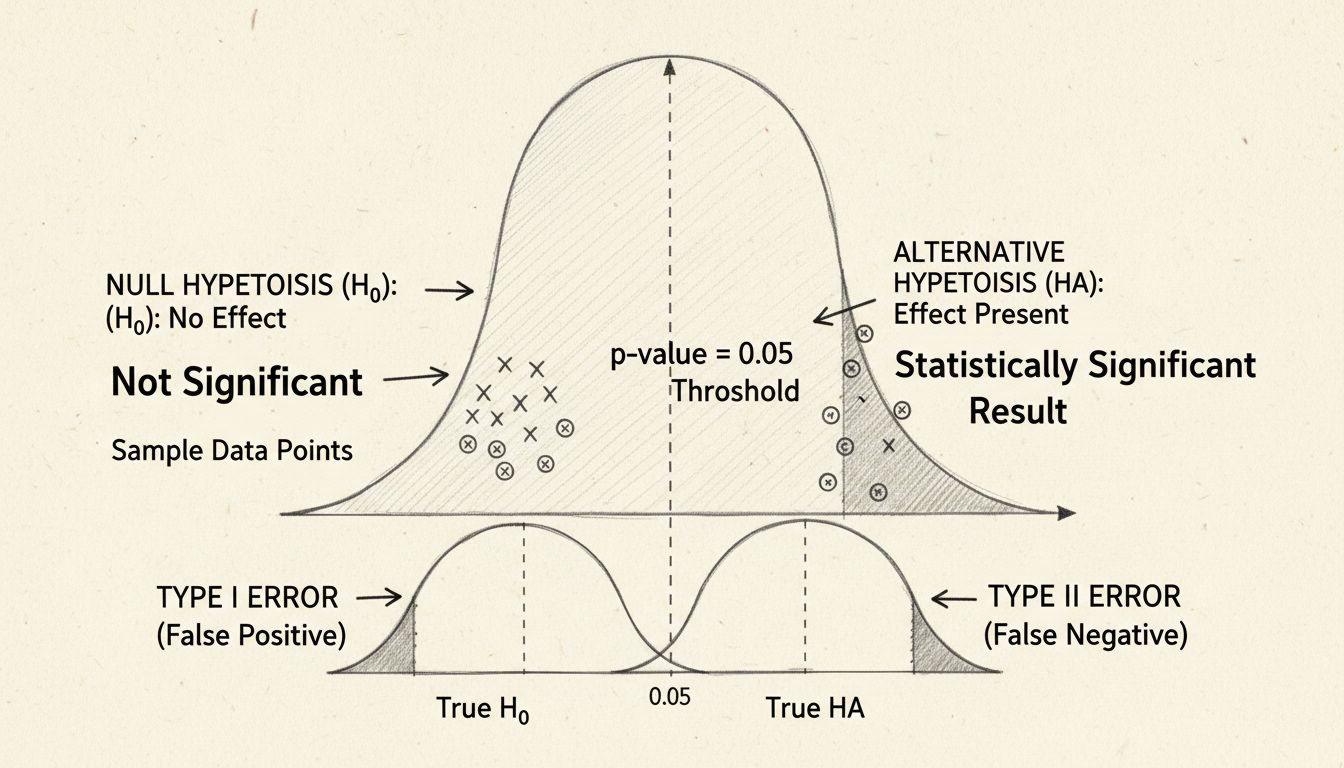
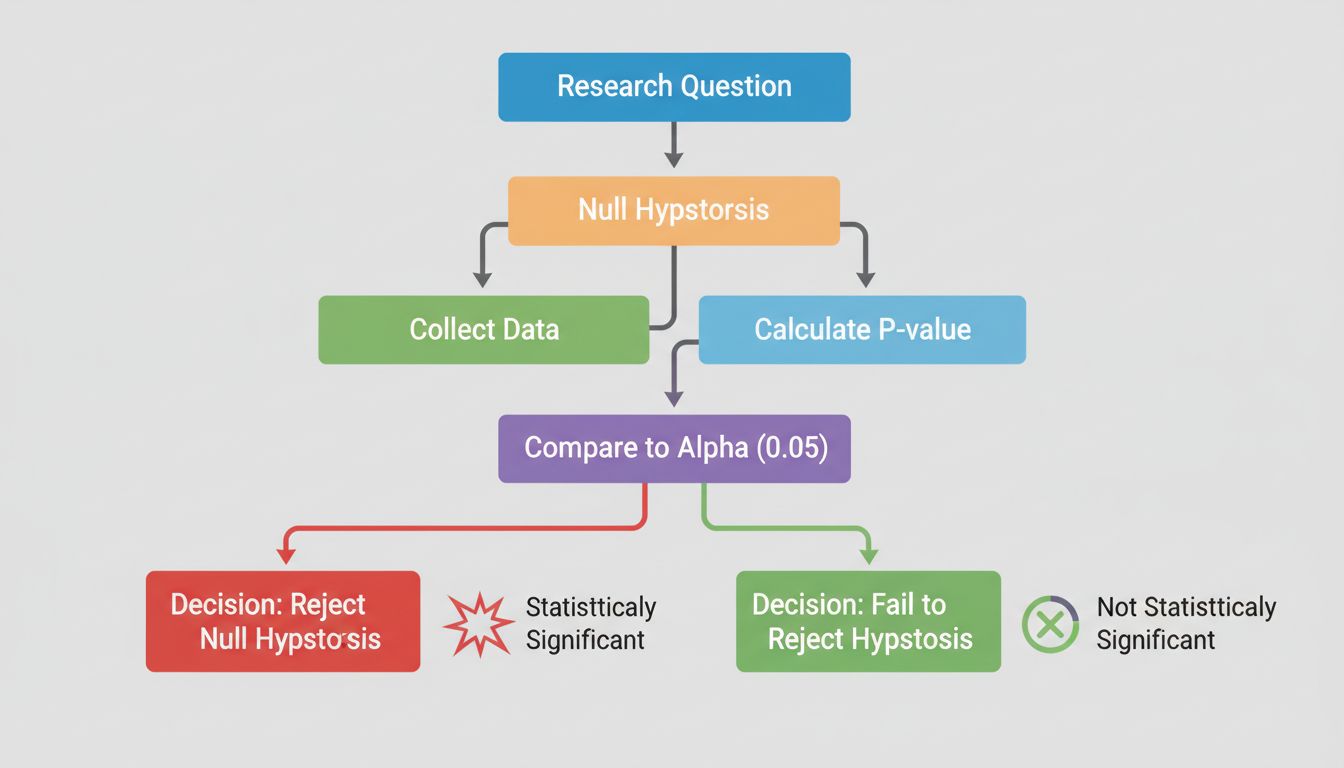
At the heart of statistical significance lies hypothesis testing, a structured methodology for evaluating claims about your data. The process begins with formulating two competing hypotheses: the null hypothesis and the alternative hypothesis. The null hypothesis assumes that there is no real effect or difference between the groups you’re studying—essentially, it represents the status quo or the assumption that any observed difference is purely due to random chance. The alternative hypothesis, by contrast, proposes that a real effect or difference does exist.
Consider a practical example: you’re testing whether a new affiliate marketing campaign generates higher conversion rates than your existing approach. Your null hypothesis would state that both campaigns produce identical conversion rates, while your alternative hypothesis would claim that the new campaign performs differently. The statistical test then evaluates which hypothesis the data supports more strongly. This framework prevents researchers and analysts from simply cherry-picking results that confirm their expectations; instead, it requires them to prove that their findings are unlikely to have occurred by random chance.
The beauty of hypothesis testing is its objectivity. Rather than relying on subjective judgment, you use mathematical calculations to determine whether your data provides sufficient evidence to reject the null hypothesis. If the evidence is strong enough, you can confidently claim that your observed effect is statistically significant—meaning it’s unlikely to be a fluke.
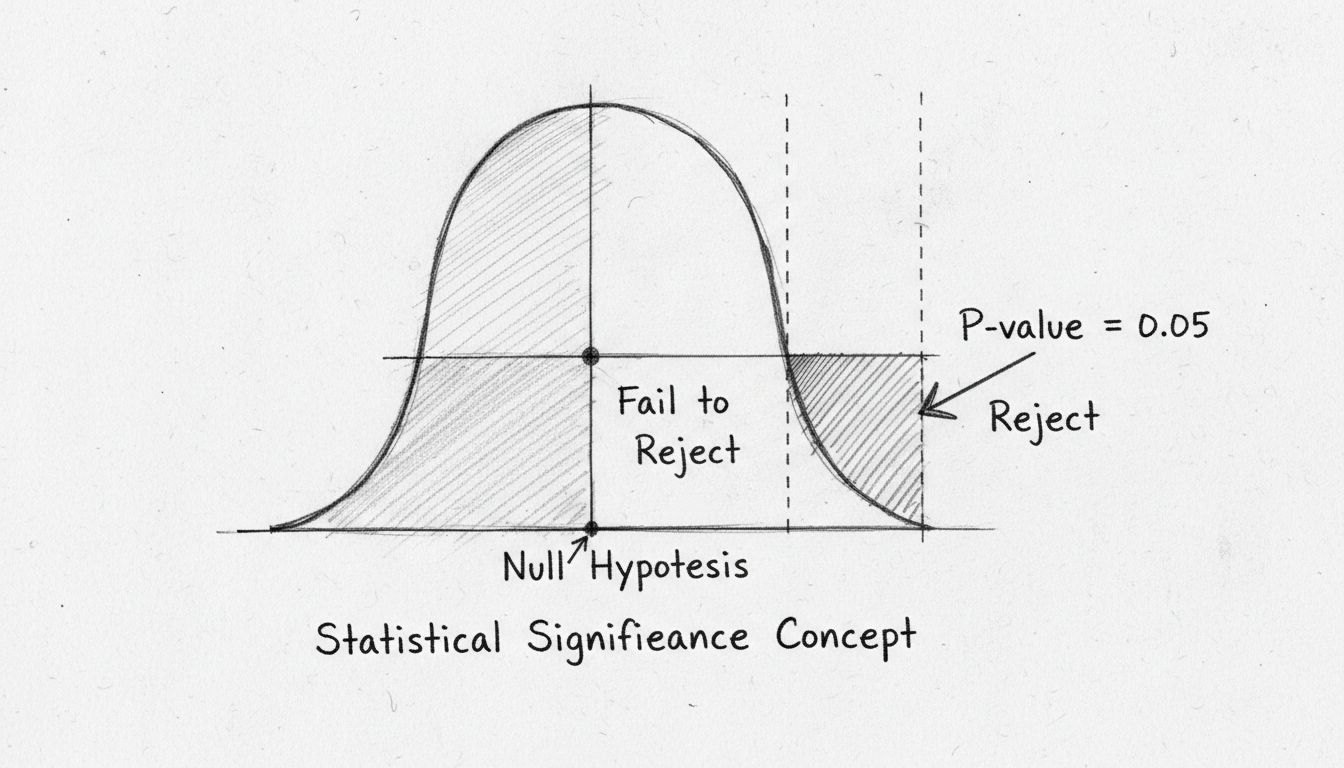
The p-value is perhaps the most widely used metric in statistical significance testing, yet it’s frequently misunderstood. The p-value represents the probability of observing your results (or results even more extreme) if the null hypothesis were actually true. In other words, it answers the question: “How likely is it that I would see this data if there really were no effect?” A small p-value indicates that your observed results would be very unlikely under the null hypothesis, suggesting that the null hypothesis is probably false and your effect is real.
The conventional threshold for statistical significance is a p-value of 0.05 or less, which translates to a 5% probability that your results occurred by chance. This means you’re willing to accept a 5% risk of incorrectly rejecting the null hypothesis when it’s actually true (called a Type I error). However, this threshold is somewhat arbitrary and varies by field and context. In medical research, where the consequences of false positives can be severe, researchers often use a more stringent threshold of 0.01 (1%). Conversely, in exploratory research or early-stage testing, a threshold of 0.10 (10%) might be acceptable.
| P-Value Range | Interpretation | Typical Action |
|---|---|---|
| p < 0.01 | Highly significant | Strong evidence against null hypothesis |
| 0.01 ≤ p < 0.05 | Significant | Moderate evidence against null hypothesis |
| 0.05 ≤ p < 0.10 | Marginally significant | Weak evidence against null hypothesis |
| p ≥ 0.10 | Not significant | Insufficient evidence to reject null hypothesis |
It’s crucial to understand what a p-value does not tell you. A p-value of 0.03 does not mean there’s a 97% probability that your hypothesis is true. It also doesn’t measure the size or practical importance of your effect. A statistically significant result can still represent a trivially small effect that has little real-world impact. This distinction between statistical significance and practical significance is one of the most common sources of confusion in data analysis.
While p-values tell you whether an effect exists, confidence intervals provide crucial information about the magnitude and precision of that effect. A confidence interval is a range of values that likely contains the true effect size, calculated with a specified level of confidence (typically 95%). If you’re testing whether a new affiliate program feature increases commissions, a 95% confidence interval might indicate that the true increase is between 2% and 8%, with 95% confidence that the true value falls within this range.
Confidence intervals offer several advantages over p-values alone. First, they communicate both the direction and magnitude of an effect, giving you a more complete picture of your results. Second, they help you assess practical significance—even if an effect is statistically significant, if the confidence interval shows the effect is negligibly small, it may not warrant implementation. Third, narrow confidence intervals indicate precise estimates, while wide intervals suggest greater uncertainty in your findings.
Effect size measures the strength of the relationship between variables or the magnitude of the difference between groups. Common effect size measures include Cohen’s d (for comparing means), correlation coefficients, and odds ratios. An effect can be statistically significant but have a small effect size, meaning the practical impact is minimal. Conversely, a large effect size might not reach statistical significance if your sample size is too small. Professional analysts always report effect sizes alongside p-values to provide a complete picture of their findings.
Sample size plays a critical role in determining statistical significance. Larger samples provide more information about your population and reduce the impact of random variation, making it easier to detect true effects. Conversely, small samples are more susceptible to random fluctuations, which can lead to either false positives (detecting an effect that doesn’t exist) or false negatives (missing an effect that does exist).
The relationship between sample size and statistical power is fundamental to research design. Statistical power is the probability of correctly rejecting the null hypothesis when it’s actually false—essentially, your ability to detect a real effect. Most researchers aim for a power of 0.80 (80%), meaning they’re willing to accept a 20% chance of missing a real effect. To achieve this power level, you need a sufficiently large sample size, which depends on the expected effect size, the significance level you choose, and the type of statistical test you’re using.
Before conducting any study or experiment, researchers should perform a power analysis to determine the required sample size. This prevents wasting resources on studies that are too small to detect meaningful effects, while also avoiding unnecessarily large studies that consume excessive time and money. In the context of affiliate marketing, this means determining how many conversions or clicks you need to observe before you can confidently conclude that a campaign change has a real impact.
Different research questions and data types require different statistical tests. The choice of test depends on factors including the number of groups being compared, whether the data is normally distributed, whether samples are independent or paired, and the type of outcome variable (continuous, categorical, etc.).
Student’s t-test compares the means of two groups and is one of the most commonly used tests. It’s appropriate when you have continuous data (like revenue amounts) and want to determine if two groups differ significantly. The test accounts for variability within each group and the sample sizes, producing a t-statistic that’s compared to a critical value to determine significance.
Chi-squared test is used for categorical data to determine whether observed frequencies differ significantly from expected frequencies. If you’re analyzing whether affiliate channel (email, social media, display ads) affects conversion rates, a chi-squared test would be appropriate.
ANOVA (Analysis of Variance) extends the t-test to compare means across three or more groups simultaneously. This prevents the problem of multiple comparisons, where conducting many separate tests increases the likelihood of false positives.
Mann-Whitney U test and Wilcoxon rank-sum test are non-parametric alternatives used when data doesn’t meet the assumptions of parametric tests, such as when data is not normally distributed.
In the business world, statistical significance guides critical decision-making across numerous functions. Marketing teams use A/B testing with statistical significance to determine whether website changes, email subject lines, or ad creatives genuinely improve performance metrics. Rather than relying on gut feelings or small sample observations, data-driven companies establish significance thresholds before running tests, ensuring that decisions are based on reliable evidence.
For affiliate marketing specifically, statistical significance helps you identify which affiliates, campaigns, and promotional strategies truly drive revenue versus those that appear successful due to random variation. When you’re evaluating whether a new commission structure increases affiliate performance, statistical testing prevents you from making expensive changes based on short-term fluctuations. PostAffiliatePro’s advanced analytics platform enables you to track affiliate metrics with the statistical rigor needed to make confident optimization decisions.
In pharmaceutical and medical research, statistical significance determines whether new treatments are effective enough to warrant approval and use. Clinical trials must demonstrate that a drug’s benefits are statistically significant before it can be prescribed to patients. The stakes are high, which is why medical research typically uses more stringent significance levels than other fields.
One of the most pervasive misconceptions is that statistical significance proves causation. A statistically significant correlation between two variables does not mean one causes the other. The classic example is the strong correlation between Nicolas Cage movie releases and swimming pool drownings—clearly, one doesn’t cause the other. Statistical significance only indicates that a relationship is unlikely to be due to chance; establishing causation requires additional evidence, such as a logical mechanism, temporal ordering, and controlled experiments.
Another common error is p-hacking or data dredging, where researchers conduct numerous statistical tests on the same dataset until they find significant results. This practice artificially inflates the likelihood of false positives because with enough tests, you’re bound to find something significant by chance alone. If you conduct 20 independent tests at a 0.05 significance level, you’d expect to find approximately one false positive result purely by chance. Responsible researchers pre-specify their hypotheses and statistical tests before analyzing data, preventing this problem.
Misinterpreting non-significant results is another pitfall. A non-significant result doesn’t prove that no effect exists; it simply means you don’t have sufficient evidence to reject the null hypothesis. This could be due to insufficient sample size, high variability in the data, or a genuinely absent effect. The absence of evidence is not evidence of absence.
The field of statistics continues to evolve, with growing recognition of limitations in traditional p-value-based approaches. Many statisticians now advocate for a more nuanced approach that combines p-values with effect sizes, confidence intervals, and Bayesian methods. Bayesian statistics, which incorporates prior knowledge and updates beliefs based on observed data, offers an alternative framework that some researchers find more intuitive and flexible than frequentist approaches.
Sequential testing and adaptive designs have gained prominence, allowing researchers to monitor results as data accumulates and make decisions about continuing, modifying, or stopping studies based on interim analyses. This approach is particularly valuable in business contexts where decisions need to be made quickly. Tools like Statsig’s Stats Engine implement sequential testing with false discovery rate control, enabling faster and more accurate decision-making during experiments.
The replication crisis in science has also highlighted the importance of understanding statistical significance correctly. Many published findings fail to replicate, partly because researchers and journals have focused excessively on achieving statistical significance while ignoring effect sizes and practical significance. Moving forward, the emphasis is shifting toward transparency, pre-registration of studies, and reporting of all results regardless of significance.
To use statistical significance effectively, establish your significance level and sample size requirements before conducting your analysis. This prevents the temptation to adjust thresholds after seeing results. Always report effect sizes and confidence intervals alongside p-values to provide a complete picture of your findings. Consider the practical significance of your results—a statistically significant effect might be too small to matter in real-world applications.
Be transparent about your methodology, including how you handled missing data, outliers, and multiple comparisons. If you conducted multiple tests, apply appropriate corrections like the Bonferroni correction to maintain your overall significance level. Document your analysis process and be willing to share your data and code with others for verification and replication.
Finally, remember that statistical significance is a tool, not a destination. It helps you make better decisions by reducing the influence of random chance, but it should be combined with domain expertise, practical considerations, and business judgment. In affiliate marketing, statistical significance helps you identify which strategies genuinely improve performance, but you should also consider factors like implementation costs, affiliate satisfaction, and long-term sustainability when making strategic decisions.
PostAffiliatePro's advanced analytics and reporting tools help you track affiliate performance with statistical rigor. Understand which campaigns truly drive results and optimize your affiliate program based on reliable data insights.

Discover why statistical significance matters in data analysis, research, and business decisions. Learn about p-values, hypothesis testing, and how to interpret...
Statistical significance expresses the reliability of measured data, helping businesses distinguish real effects from chance and make informed decisions, especi...
Master A/B testing for betting affiliates: learn p-values, confidence levels, sample sizes, and strategies to optimize conversions.
Cookie Consent
We use cookies to enhance your browsing experience and analyze our traffic. See our privacy policy.